Sudoku: Naked Multiples in Excel

This blog post is about the modelling of Sudoku naked multiples in Excel. It concerned with the user input / decisions and how the model uses this information to evaluate its validity in respect of the puzzle in its current state.

The concept of naked pairs, triples, quods etc and how they operate in Sudoku is best explained by experts. I suggest Hodoku or Kristanix. The web sites address the issues from slightly different perspectives but both are very clear.

Sudoku dimensions

Sudoku  has three dimension (row, column and sub-grid). Naked multiples operate in all three of the dimensions, but can only be evaluated one dimension at a time. In this model the first user choice is to decide on the dimension he wishes to investigate.

Select the orientation of the Naked Multiple analysis

This registration process calls a copy of an incomplete Excel template and creates a model for solving a discrete element of the Sudoku puzzle. The user must link the template to the original puzzle and the latest state of play for the puzzle. (It is not strictly necessary to link it to the original, but it makes the presentation easy in terms of identifying progress made.) The initial view of the working paper is shown below. It is identical in the cases of each of the three dimensions.

Joining the template to previous parts of the model

From here forwards,the spreadsheet presentation depends on the dimension
orientation of the template that you initially selected. The choices range from 1 to 9. 

The choice of Column or Row number is obvious.

While for row and columns it is obvious which row or column number to choose, it is less so for the sub-grid numbering, The sub-grid template includes a numbering layout.

Sub-grid numbering

Analysis by Column

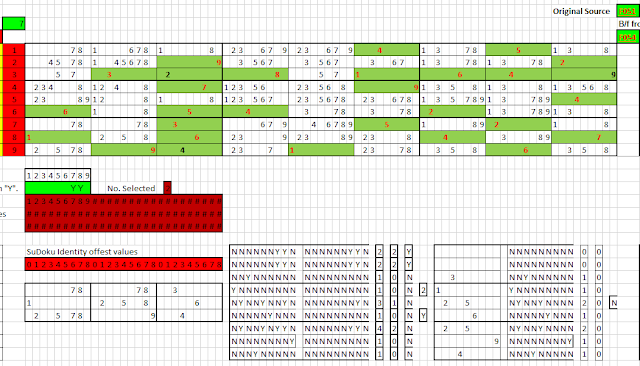
This explanation has a starting point equivalent to column 6 in the Sudoku grid above. The picture below shows the same column picked out for detailed analysis. It highlights the Sudoku identities 3, 6 & 8, which, in this case, make up a Naked Triple. The player must mark these 3 Ids with a "Y" in the green input grid.

The user marks up the green input grid.

The remainder of this worksheet is given over to validation and analysis.

Validation

This evaluates whether the player selected a bona fide naked triple and, if so, considers whether it leads to a solution of one or more cells. In keeping with many non numeric analyses the logic can be long winded. The diagram below marks each of the analytical groups of cells or ranges with an identifying letter.

Validation and analysis by column - with identifying letters

Task Id	Description	Functionality
A	Inspection column	This is simply a repeat of the column selected at the top of the template, but without the formatting.
B	Current Id's	For each cell within the column the Identities currently available to it are shown. This includes solved cells.
C	Id's for inspection	This shows each cell which contains an Id that has been specified by the played / user as for inspection.
D	Identity count	For each cell, a count of the number of identities available to it. Cells with a count of 1 are solved. If the count is zero, there is an error.
E	Selected Id count	This is a count of the identities within the cell that are also flagged for inspection.
F	Id count & selected Id count equal	Phase 1 of the validation, evaluates whether the number of identities available to the cell and the number of selected identities are equal. Where this is true, the cell is set to "Y".
G	Validation complete	This covers two small processes. The first is a count of the Task Id F processes set to "Y". The second evaluates whether this count is the same as the number of Sudoku Identities selected for inspection. If this is true the validation is complete and the cell marked "Y". Failure at this point effectively stops further analysis.
H	Inspection column - less triples	This is simply a repeat if Task Id A, without any Sudoku Id associated with the validated triple. This means that the cells for the triple itself are left empty.
I	Identities after Task Id H	This is equivalent to Task Id B, it shows only those Sudoku identities that left. Where appropriate the Sudoku Id cells is marked "Y".
J	Identity count after Task I	This shows the count of Sudoku Id's in each cell after the removal of the naked multiple. Of course, this count will be 0, for the naked cells themselves.
K	Solved?	This analysis answers the question of whether the removal of the Ids associated with the naked triple generates a solution to the cell - in effect a clear result. The value 1 indicates that it did and 0 it did not.
L	Inspection column - post analysis	The naked triple cells are reinstated within the inspection column.
M	Stop cell	This takes the sum of Task Id K. If it is greater than zero, it stops any further analysis in this phase.

In theory, the player can undertake more than one naked multiple analysis within a single dimension consecutively. The Excel model permits this but only if there is no clear result from the first phase.

In this case, we did generate a clear result in the 8th row of the column under inspection. This is shown in the output Sudoku grid.

The processes involved with naked multiple analysis by Row and by Sub-Grid are identical, but their shapes on the Excel page look different to take account of the orientation within the Sudoku puzzle. A diagram of the Sub-grid page shows how different the Excel sheet looks.

Note that this analysis, although successful in showing surplus Identities did not deliver a final result.